.
İnsanlık yıldızlara baktığından beri sonsuzluk kavramı aklımıza kuvvetle girmiştir. Hayal gücümüzün ötesinde olan, ulaşılmaz ve anlaşılmaz olan… Tüm bunlar ve çok daha fazlası aslında sonsuzluktur.
Ama matematikte sonsuzluk uzun bir yol kat ediyor. Bu kavramı en yoğun şekilde inceleyen ve kitabımda da anlattığım gibi Alman matematikçi Georg Cantor olmuştur. sonsuzluğun tarihicanavarı evcilleştirmeyi başardı.
Cantor’un, diğerlerinin yanı sıra, farklı boyutlarda sonsuzluklar olduğundan emin olmasına izin veren argümanları vardı. Bu nasıl mümkün olaiblir?
Vikipedi
sayılabilenin sonsuzluğu
Setlerin boyutlarını karşılaştırmak için muhtemelen en kolay teknik kibrit nesneleri birbirinden Bir kümenin her bir elemanı diğerinin bir elemanı ile eşleştirilirse (ve hiçbiri geride kalmazsa), her iki kümenin de aynı sayıda elemana sahip olmasını, yani aynı boyuta sahip olmasını sağlayabiliriz. Matematikte bir yapı oluşturduğumuzu söyleriz. birebir örten.
Bu eşleştirme tekniği, sonlu kümelerle çok iyi çalışır. Bir şeyleri saymak, ilk doğal sayılar ile saymak istediğimiz şey arasında bir nijeksiyon oluşturmaktan başka bir şey değildir.
Ancak tahminler, sonsuz kümelerin boyutlarını karşılaştırmanın da iyi bir yoludur. Ve sonsuzluktan bahsedecek olursak, akla ilk gelen küme, Tümü doğal sayılar Doğallarla ikiye bölünebilen herhangi bir kümenin olduğu söylenir. sayılabilir.
Ancak sezgilerimiz bize oyun oynayabilir. Cantor’un karşılaştığı bazı örneklere bakalım.
Rasyonel sayılar, tam sayıların oluşturduğu kesirlerdir (payda sıfırdan kaçınarak). Bu şekilde, özellikle tüm doğal sayılar rasyoneldir. Ama… kaç tane rasyonel var?
Cantor’un henüz bir öğrenciyken ve sadece eğlence için ispatladığı sonsuzlukla ilgili ilk sonuçlardan biri, gerçekte rasyonel sayılar kadar doğal sayı olduğuydu. Ve bu, birinin diğerinin parçası olmasına rağmen.
Bunu kontrol etmek, rasyonellerin bir listesini vermeye, yani hangisinin birinci, ikinci olduğunu vb. tespit etmeye eşdeğerdir. , çünkü her zaman yapabiliriz: sıfır, pozitif, negatif, pozitif, negatif,…).
Cantor’a atfedilen argüman basit ama etkilidir. Paydası 1 olan tüm rasyonelleri üst üste, paydası 2 olanları ikinci sıraya, paydası 3 olanları üçüncü sıraya koyarız. Bu şekilde, bir tür sonsuz tabloda tüm rasyonellere sahip olacağız, ancak tekrarlanan birçok şey olacak (önemli değil, daha sonra kaldırılacaklar). Şimdi, tablodaki tüm sayıların içinden geçen basit bir zikzak çizgisi bir numaralandırma işlevi görecektir.
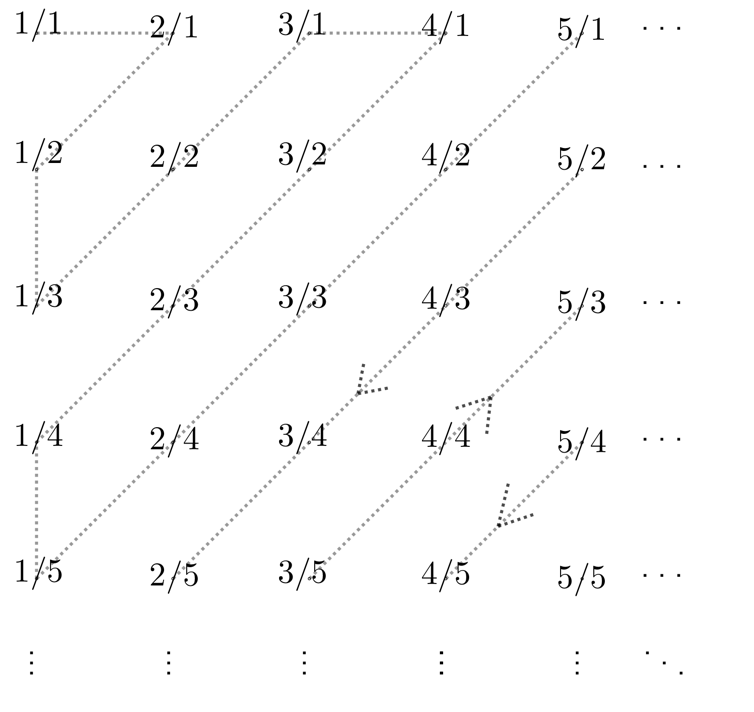
kendi detaylandırma
O halde, ne kadar rasyonel sayı varsa o kadar doğal sayı vardır.
Sürekliliğin sonsuzluğu
Ancak tüm rasyonel sayıları doğruya çizersek, pratik olarak onu doldurdukları ortaya çıkar. Aslında herhangi bir (reel) sayıya istediğimiz kadar yakın bir rasyonel sayı vardır. Bu özellik olarak bilinir yoğunluk rasyonellerin gerçeklere dönüşmesi.
Bu gerçeği çok iyi bilen Cantor, tüm gerçek sayıları sıralamanın mümkün olup olmayacağını merak etti. Satırı doldurmak için rasyonellerin eksikliği pratikte hiçbir şey gibi göründüğü için, bu çok doğal bir sorudur (kelime oyunu amaçlı).
Tüm gerçek sayıları değil, 0 ile 1 arasında olanları tutacağız. Bu sayıların bir özelliği var: Tümü 0’dan başlayarak ondalık biçimde yazılabilirler (1=0.999… olduğunu unutmayın).
Cantor aşağıdaki argümanı önerir. 0 ile 1 arasındaki tüm gerçek sayıları sıralayabileceğimizi ve bir listeye koyabileceğimizi varsayalım. Örneğin:
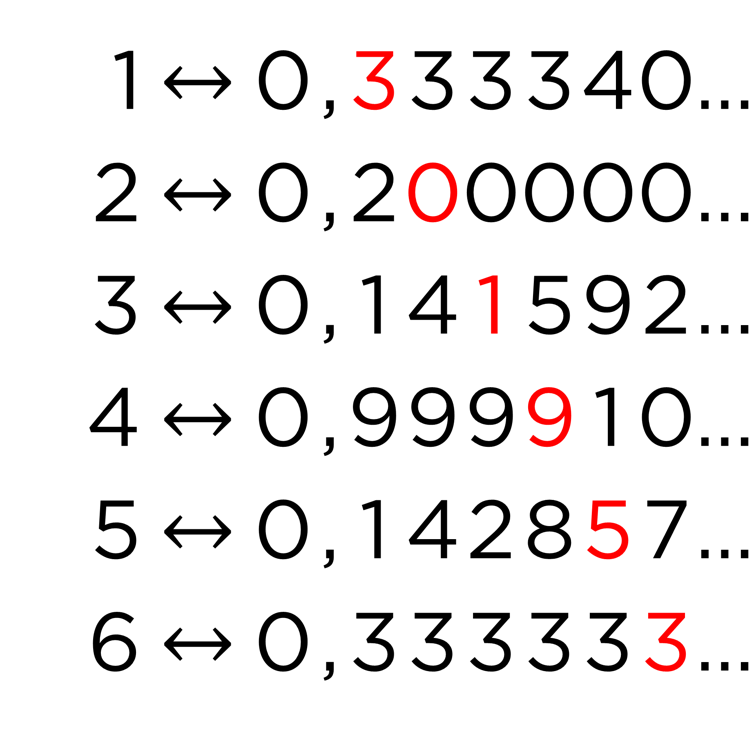
kendi detaylandırma
Cantor bu listeye göre yeni bir numara oluşturuyor.
İlk sayının (kırmızı olan) ilk ondalık basamağına bakalım, bu durumda 3. Cantor, numarası için herhangi bir basamağı ilk ondalık sayı olarak alır. HAYIR 3 örneğin 4 olsun.
Argümanı ikinci sayının ikinci ondalık basamağı olan 0 ile tekrarlıyoruz; Cantor örneğin 1 alır. Üçüncü sayının üçüncü ondalık basamağı 1 olduğu için sayımız olarak örneğin 2 alırız. Ve böylece listedeki tüm numaralarla devam ediyoruz. Bu şekilde 0.412064 sayısını oluşturuyoruz…
Ama bu sayı hakkında bu kadar özel olan ne? ne olmuş HAYIR listede. Nitekim ilk ondalık sayı listedeki ilk sayıdan farklı olduğu için ilk sayı olamaz; ikinci ondalık sayı listedeki ikinciden farklı olduğu için ikinci de olamaz; ne de üçüncü, çünkü üçüncü ondalıktan farklıdır; Dördüncü değil, beşinci değil…
Kısacası, Cantor’un gösterdiği şey, 0 ile 1 arasındaki sayıları numaralandırmanın yolu ne olursa olsun, her zaman en az birini kaçıracağımızdır. Başka bir deyişle, ortaya çıkıyor imkansız gerçekler (0 ile 1 arasında) ve doğallar arasında bir eşleştirme oluşturun.
Ve doğal sayılardan daha fazla gerçek sayı olduğu için Cantor, sürekliliğin sonsuzunun, gerçek sayıların sonsuzunun, doğal sayıların sonsuzundan daha büyük olduğu sonucuna varır.
Farklı boyutlarda sonsuzluklarımız var.
Her biri bir öncekinden daha büyük bir dizi sonsuzluk
Bu Cantor argümanı, yayınladığı ilk argüman değildi. Orijinali çok daha karmaşık ve teknikti ve pek çok aksilik getirdi (bu hikayeyi ayrıca sonsuzluğun tarihi).
Bunu telafi etmek için, köşegen argümanı (gördüğümüzün bilindiği gibi) aslında herhangi bir veriden daha büyük bir sonsuzluk üretmenin bir yolunu sunar. olarak bilinen şey budur Cantor teoremi.
Cantor, yalnızca diğerinden daha büyük bir sonsuzun varlığını kanıtlamakla kalmaz. Her biri bir öncekinden daha büyük olan bir dizi sonsuzluk olduğunu gösterir.
.









