.

Imagens Getty
A Signal Foundation, criadora do Protocolo Signal que criptografa mensagens enviadas por mais de um bilhão de pessoas, lançou uma atualização projetada para se preparar para uma perspectiva muito real que nunca está longe dos pensamentos de quase todos os engenheiros de segurança do planeta: o queda catastrófica dos protocolos criptográficos que protegem alguns dos segredos mais confidenciais da atualidade.
O Protocolo Signal é um ingrediente chave nos mensageiros Signal, Google RCS e WhatsApp, que juntos têm mais de 1 bilhão de usuários. É o mecanismo que fornece criptografia de ponta a ponta, o que significa que as mensagens criptografadas com os aplicativos podem ser descriptografadas apenas pelos destinatários e por mais ninguém, incluindo as plataformas que habilitam o serviço. Até agora, o Signal Protocol criptografava mensagens e chamadas de voz com X3DH, uma especificação baseada em uma forma de criptografia conhecida como Elliptic Curve Diffie-Hellman.
Um breve desvio: WTF é ECDH?
Muitas vezes abreviado como ECDH, Elliptic Curve Diffie-Hellman é um protocolo próprio. Ele combina dois blocos de construção principais. A primeira envolve o uso de curvas elípticas para formar pares de chaves assimétricas, cada uma delas exclusiva para cada usuário. Uma chave do par é pública e está disponível para qualquer pessoa usar para criptografar mensagens enviadas ao seu proprietário. A chave privada correspondente é guardada de perto pelo usuário. Ele permite ao usuário descriptografar as mensagens. A criptografia que depende de um par de chaves pública-privada é frequentemente conhecida como criptografia assimétrica.
A segurança da criptografia assimétrica é baseada em funções matemáticas unidirecionais. Também conhecidas como funções de alçapão, esses problemas são fáceis de calcular em uma direção e substancialmente mais difíceis de calcular no sentido inverso. Na criptografia de curva elíptica, esta função unidirecional é baseada no problema do Logaritmo Discreto em matemática. Os principais parâmetros são baseados em pontos específicos de uma curva elíptica, que é definida como o corpo de inteiros módulo primo P.
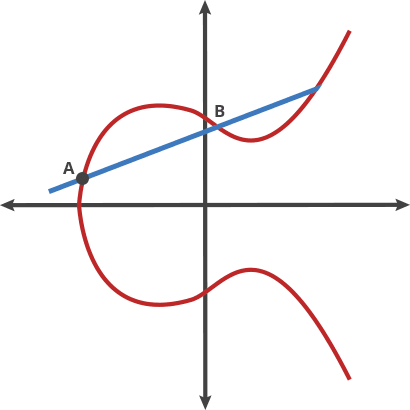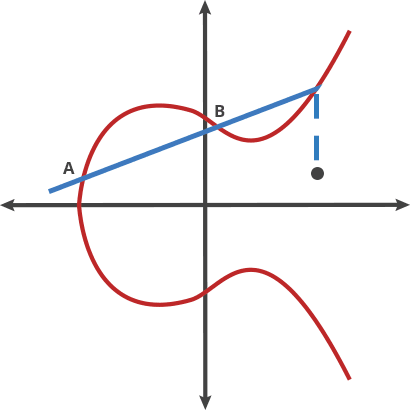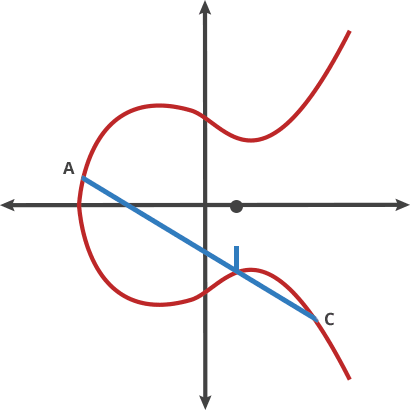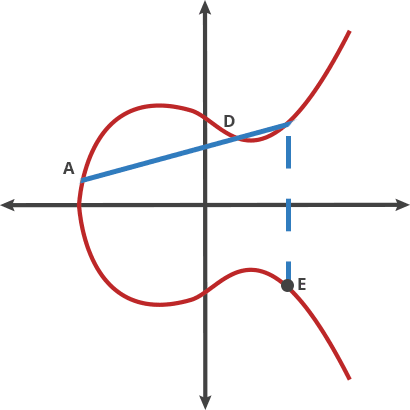
Quando alguém conhece o ponto inicial (A) na imagem acima, mostrando uma curva elíptica e o número de saltos necessários para chegar ao ponto final (E), é fácil saber onde está (E). Mas quando tudo o que alguém sabe são os pontos inicial e final, é quase impossível deduzir quantos saltos são necessários.
Conforme explicado em um artigo da Ars de 2013:
Vamos imaginar esta curva como cenário para um bizarro jogo de bilhar. Pegue quaisquer dois pontos da curva e desenhe uma linha através deles; a linha cruzará a curva exatamente em mais um lugar. Neste jogo de bilhar, você pega uma bola no ponto A e a lança em direção ao ponto B. Quando ela atinge a curva, a bola salta para cima (se estiver abaixo do eixo x) ou para baixo (se estiver acima do eixo x). -axis) para o outro lado da curva.
Podemos chamar esse movimento de bilhar em dois pontos de “ponto”. Quaisquer dois pontos em uma curva podem ser pontilhados para obter um novo ponto.
Um ponto B = C
Também podemos encadear movimentos para “pontilhar” um ponto consigo mesmo repetidamente.
Um ponto A = B
Um ponto B = C
Um ponto C = D
…
Acontece que se você tem dois pontos, um ponto inicial “pontilhado” consigo mesmo n vezes para chegar a um ponto final, descobrir n quando você só conhece o ponto final e o primeiro ponto é difícil. Para continuar a nossa bizarra metáfora do bilhar, imagine que uma pessoa joga o nosso jogo sozinha numa sala durante um período de tempo aleatório. É fácil para ele bater na bola repetidamente seguindo as regras descritas acima. Se alguém entrar na sala mais tarde e vir onde a bola foi parar, mesmo que conheça todas as regras do jogo e onde a bola começou, não poderá determinar o número de vezes que a bola foi rebatida para chegar lá sem passar pelo jogo inteiro novamente até que a bola chegue ao mesmo ponto. Fácil de fazer, difícil de desfazer. Esta é a base para uma função de alçapão muito boa.
.








