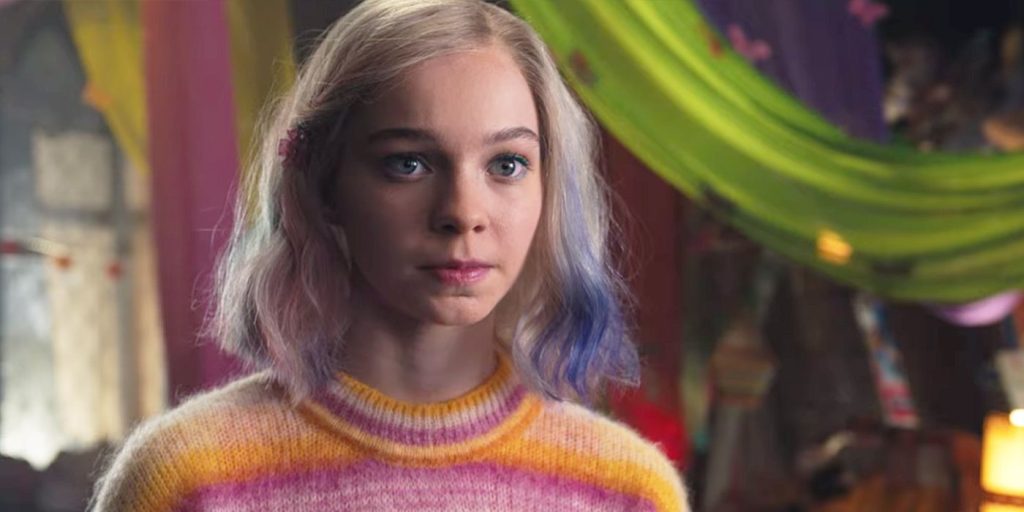.
Emma Myers, de quarta-feira, estrelará ao lado de Jennifer Garner, Ed Helms e Brady Noon no próximo filme de comédia de troca de corpo da Netflix, Family Leave.
Quarta-feira a estrela Emma Myers está voltando para a Netflix para o filme de comédia de troca de corpo, Licença familiar.
De acordo com o Deadline, o ator – que atualmente pode ser visto em Quarta-feira como a colega de quarto/amiga lobisomem colorida do personagem-título, Enid Sinclair – contracenará com Brady Noon (The Mighty Ducks: Game Changers), Jennifer Garner (O Projeto Adão) e Ed Helms (O escritório) dentro Licença familiarque é baseado no livro best-seller de Amy Krouse Rosenthal Hora de dormir para a mamãe. Myers interpretará CC Walker, filha de Jess (Garner) e Bill Walker (Helms) e irmão de Wyatt (Noon).
McG (A Babá: Rainha Assassina) dirigirá a próxima comédia familiar da Netflix a partir de um roteiro escrito por Adam Sztykiel (Adão Negro), com base em um rascunho anterior de Victoria Strouse (À procura de Dory). Licença familiar segue “Jess e Bill Walker, que estão fazendo o possível para manter sua família conectada à medida que seus filhos crescem, mais independentes e mais distantes. Quando um encontro casual com um leitor astrológico faz com que a família acorde para uma troca de corpo inteiro, na manhã do dia mais importante de cada uma de suas vidas, os Walker podem se unir para conseguir uma promoção, uma entrevista na faculdade, um contrato com uma gravadora e um teste de futebol?”
Os assinantes da Netflix estão adorando a quarta-feira
Criado por Smallville criadores Al Gough e Miles Millar, Quarta-feira é uma série live-action de mistério sobrenatural que segue a quarta-feira homônima (Jenna Ortega) enquanto ela frequenta a Academia Nevermore enquanto tenta dominar sua habilidade psíquica emergente, parar uma matança monstruosa que aterroriza a cidade local de Jericho e resolver um problema de 25 anos. mistério. Quarta-feira tem sido um enorme sucesso para a Netflix, com a série atualmente a caminho de se tornar o programa mais assistido do streamer. Embora a maior parte da atenção da série esteja voltada para a atuação principal de Ortega como o titular Addams, muitos fãs elogiaram a atuação de Myers como Enid, com muitos também querendo ver o ator retratar o personagem favorito dos fãs da Marvel, Spider-Gwen em um dos próximos projetos live-action da Sony.
Quarta-feira os fãs também responderam positivamente à notícia de que as co-estrelas Ortega e Percy Hynes White estão estrelando juntos uma comédia romântica intitulada Inverno Primavera Verão ou Outono. Depois que as fotos vazadas do filme ainda a ser anunciado começaram a circular online, os fãs foram às mídias sociais para expressar o quão empolgados estavam com as estrelas interpretando interesses amorosos em Inverno Primavera Verão ou Outono depois Quarta-feira apresentou um relacionamento de flerte entre os respectivos personagens dos atores.
Toda a primeira temporada de Quarta-feira está disponível para transmissão na Netflix.
Fonte: Prazo
.