.
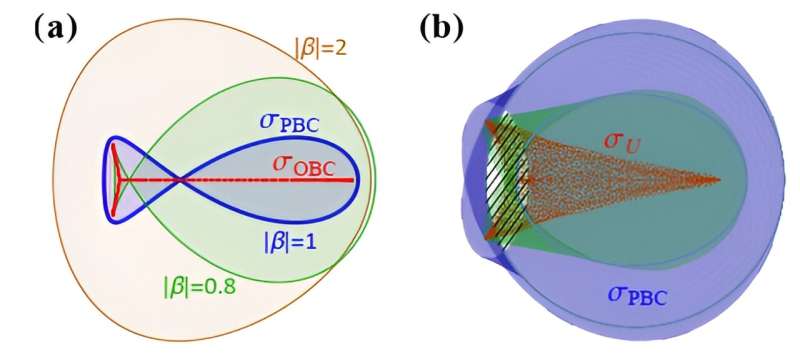
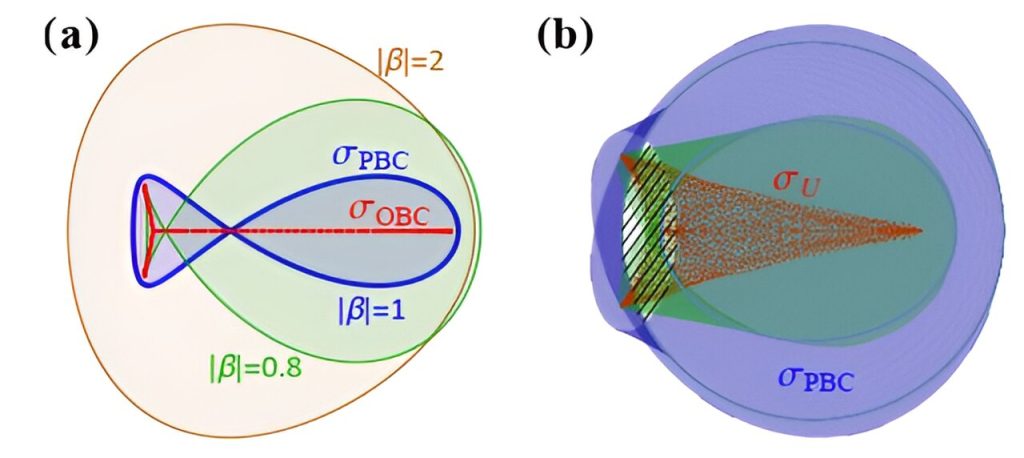
À esquerda, espectros de energia típicos para sistemas não-Hermitianos 1D sob condições de contorno periódicas ou abertas aparecem como loops (azul) com enrolamentos espectrais e arcos (vermelho). À direita, espectros de energia sob condições de contorno aberto (vermelho) para sistemas não-Hermitianos de dimensões superiores são derivados daqueles sob condições de contorno periódicas (azul) pela eliminação dos enrolamentos espectrais. Crédito: Science China Press
Um estudo, publicado na revista Boletim Científico e liderado pelo Dr. Haiping Hu do Instituto de Física da Academia Chinesa de Ciências (IOP, CAS), explora o efeito de pele não-Hermitiano (NHSE) e as bandas não-Bloch.
A física não-hermitiana é um campo em rápido crescimento que fez um progresso notável nos últimos anos. O NHSE é um fenômeno paradigmático de sistemas não-hermitianos, marcado pelo acúmulo extensivo de autoestados nas fronteiras e pela extrema sensibilidade dos espectros de energia às condições de fronteira. O NHSE desafia a teoria tradicional da banda de Bloch e oferece novas maneiras interessantes de controlar fenômenos de onda e projetar dispositivos funcionais.
NHSE pode ocorrer em diferentes dimensões espaciais e está intimamente relacionado às condições de contorno aberto (OBC) do sistema. Em uma dimensão (1D), o OBC é definido, tornando o NHSE bem compreendido e descritível pela teoria de banda não Bloch. No entanto, em dimensões mais altas, a diversidade de geometrias de rede complica o OBC.
Questões fundamentais sobre NHSE em dimensões superiores permanecem sem resposta, tais como: Como espectros de energia e efeitos de pele podem ser sistematicamente contabilizados em várias geometrias de rede? Qual é a origem topológica de NHSE em dimensões superiores? Como os modos de pele associados a diferentes cortes de rede são interconectados?
O Dr. Hu se inspirou em estudos de 1D NHSE. Em 1D, o NHSE surge de lacunas de pontos, onde espectros de energia sob condições de contorno periódicas formam loops no plano complexo. A obtenção de espectros não Bloch requer a eliminação dos enrolamentos causados por esses loops. O Dr. Hu revelou que, ao introduzir transformações de calibre virtual em dimensões mais altas, é possível contabilizar enrolamentos espectrais em todas as direções e, então, eliminar esses enrolamentos para obter os espectros não Bloch do sistema.
Este método produz estruturas espectrais que são independentes da geometria. O Dr. Hu demonstrou ainda que seus espectros não Bloch são equivalentes aos descritos pela renomada teoria da Ameba. Esta abordagem também revela como lidar com NHSE em diversas geometrias de rede.
Como os modos de pele são localizados nas fronteiras, é necessário continuar analiticamente os momentos da rede no Hamiltoniano de Bloch. O Dr. Hu descobriu que diferentes geometrias correspondem a diferentes escolhas de base de momento. Por meio de transformações de base, o NHSE sob diferentes geometrias pode ser gerenciado, e as propriedades dos modos de pele sob diferentes geometrias seguem relações de transformação específicas.
Este trabalho avança significativamente a compreensão e a exploração do NHSE, oferecendo diretrizes para manipular modos de pele por meio de adaptação de rede apropriada. As descobertas abrem amplos caminhos para futuras investigações teóricas e experimentais em sistemas ópticos e fotônicos, átomos frios, acústica, metamateriais e outros sistemas não conservativos.
Mais informações:
Haiping Hu, Origem topológica do efeito de pele não-hermitiano em dimensões superiores e espectros uniformes, Boletim Científico (2024). DOI: 10.1016/j.scib.2024.07.022
Fornecido pela Science China Press
Citação: Efeito de pele não hermitiano em todas as dimensões vinculado à topologia de ponto-lacuna (2024, 30 de agosto) recuperado em 30 de agosto de 2024 de https://phys.org/news/2024-08-hermitian-skin-effect-dimensions-gap.html
Este documento está sujeito a direitos autorais. Além de qualquer uso justo para fins de estudo ou pesquisa privada, nenhuma parte pode ser reproduzida sem permissão por escrito. O conteúdo é fornecido apenas para fins informativos.
.